Rasterization Triangle (Scan Conversion)
Rasterizing Polygons는 다각형을 Raserize화 시키는 방법이다. Convex Shape의 경우 쉽게 Trinagle 형태로 만들어 줄 수 있다. 반면 Concvae한 형태는 삼각형 형태로 만들기는 어렵다.
Convex set은 어떠한 두 점을 연결하더라도, 도형안에 존재하는 집합이다. 이는 나중에 자세히 다루도록 하고, 삼각형 하나에 점이 존재하는지 확인해보자.
Simple Algorithm
삼각형 안에 존재하는 영역에 점을 찍어주는 과정을 생각해보자.
단순하게 if 문을 통해 Triangle 영역 안에 있으면 점을 찍기만 하면 된다. 중요한 것은 "어떻게 삼각형 영역안에 존재하는가?"를 판단하는 것이다.
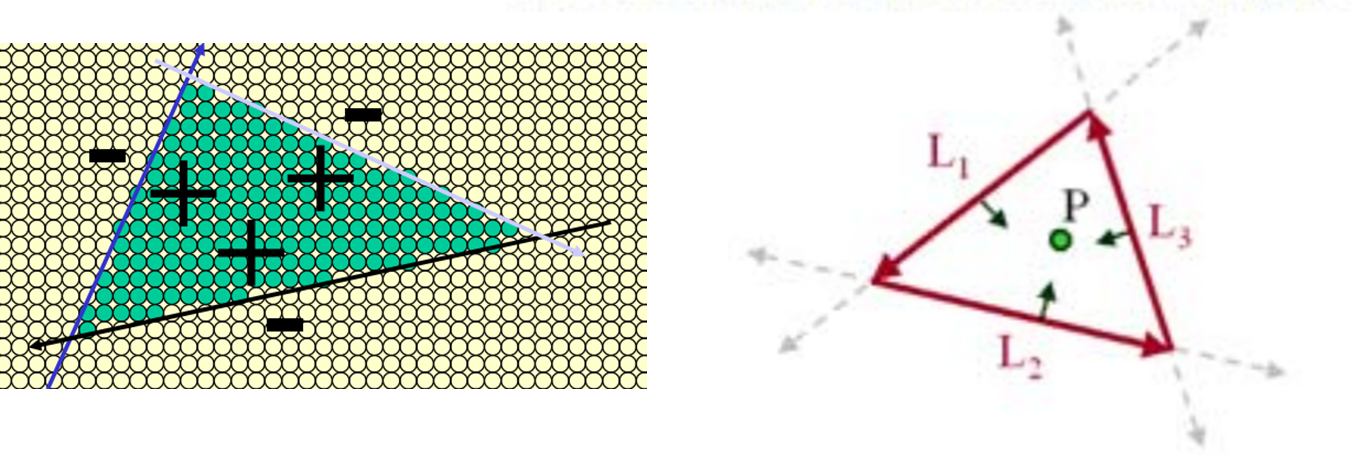
직선 방정식에서 직선 위에 영역은 +로 확인하였다. 삼각형은 3가지의 직선으로 구성되어 있으며 직선 3개 방정식에 대하여 점이 모두 양수이면 삼각형 영역 안에 존재하는 것을 알 수 있다.
출처 : Utah university cs5600 wk3 ppt
$$ \vec{L_1} = P_1-P_0 \\ \vec{L_2}=P_2-P_1 \\ \vec{L_3}=P_0-P_2 $$
이전에 있던 기억들을 다시 꺼내보면 직선 방정식은 다음과 같이 표현하였다.
$$F(x,y)=(dy)x-(dx)y+dx(B)=0 $$
여기서 B는 주어진 점에 의하여 결정 된다.
$$F(x,y)=dy(x-x_0)-dx(y-y_0)=0 \\ \therefore B=dx(y_0)-dy(x_0) $$
간단하게, min max grid를 만들고 나서 위의 조건들이 만족하는지 하나씩 확인만 해주면된다.
Sweep-Line
1번째 방법은 살짝 무식한 방법이다.1번째의 경우 사각형 영역에 대해서 모두 Searching 함으로 불필요한 점까지 Searching 한다는 단점이 존재한다. 2번째 방법으로는 Line따라서 Sweeping 하면서 가는 것이다. 이에 불필요한 영역의 Searching을 줄일 수 있다.
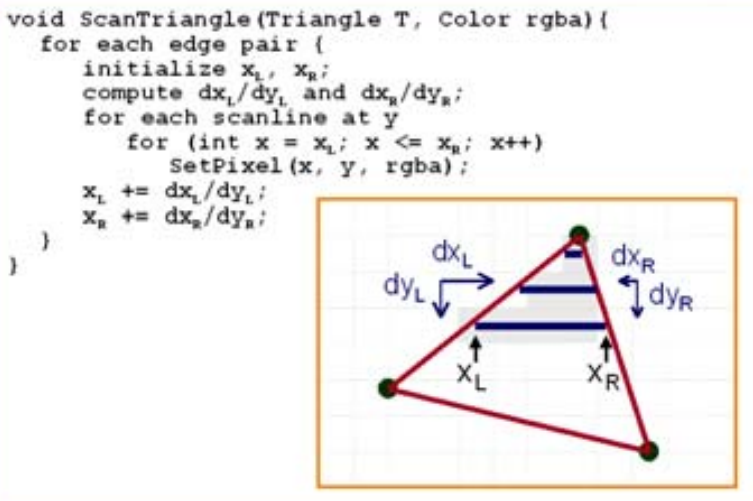
Utah Uinversity CS5600 wk3
1. 이동 방향을 정함. (l방향과 r방향을 정함)
2. 각각에 해당하는 기울기 만큼 이동한다.
3. 초기의 xl과 xr 좌표를 구함.
4. Line이 바뀌는 경우 Line Switching을 해줌.
여기에서는 1번의 경우 가정하여 풀었음.
아래 코드 참조
Convex Characteristics
Convex Set의 경우 3개의 점 기준으로 내부의 점은 다음과 같이 결정할 수 있다.
$$ P=\sum_{i=1}^3 \lambda_iP_i \\ \sum_i \lambda_i =1 \\ \forall \lambda \in [0,1] $$
즉 , Weight factor를 통하여 내부의 점을 구할 수 있다. 반대로 말하자면, 내부의 점을 통해 labmda 값을 구해서 위의 조건을 만족하면 내부의 점이 있음을 확인할 수 있다.


위의 행렬을 통해 구하는 과정은 InsideCheck 함수와 동일한 기능을 한다. 만약 matlab과 같이 Matrix에 유리한 프로그램을 사용한다면, 이 과정은 매우 쉽게 적용해볼 수 있다.
Rasterization Triangle (Simple)
import matplotlib.pyplot as plt
import numpy as np
P0=np.array([10,30])
P1=np.array([0,10])
P2=np.array([20,0])
def get_TriEq(P0,P1):
dx=P1[0]-P0[0]
dy=P1[1]-P0[1]
B=dx*P0[1]-dy*P0[0]
return (dy,-dx,B)
def InsideCheck(x,y,l1,l2,l3):
return (x*l1[0]+y*l1[1]+l1[2]>=0) and \
(x*l2[0]+y*l2[1]+l2[2]>=0) and \
(x*l3[0]+y*l3[1]+l3[2]>=0)
l1coeff = get_TriEq(P1,P0)
l2coeff = get_TriEq(P2,P1)
l3coeff = get_TriEq(P0,P2)
minx = min(P0[0],min(P1[0],P2[0]))
maxx = max(P0[0],max(P1[0],P2[0]))
miny = min(P0[1],min(P1[1],P2[1]))
maxy = max(P0[1],max(P1[1],P2[1]))
px=[]
py=[]
for x in range(minx,maxx+1):
for y in range(miny,maxy+1):
if InsideCheck(x,y,l1coeff,l2coeff,l3coeff):
px.append(x)
py.append(y)
plt.scatter(px,py)
plt.triplot([P0[0],P1[0],P2[0]],[P0[1],P1[1],P2[1]])
plt.show()
Rasterization Triangle (Sweep-Line)
import matplotlib.pyplot as plt
import numpy as np
P0=np.array([10,30])
P1=np.array([0,10])
P2=np.array([20,0])
def get_TriEq(P0,P1):
dx=P1[0]-P0[0]
dy=P1[1]-P0[1]
B=dx*P0[1]-dy*P0[0]
return (dy,-dx,B)
def InsideCheck(x,y,l1,l2,l3):
return (x*l1[0]+y*l1[1]+l1[2]>=0) and \
(x*l2[0]+y*l2[1]+l2[2]>=0) and \
(x*l3[0]+y*l3[1]+l3[2]>=0)
l1coeff = get_TriEq(P1,P0)
l2coeff = get_TriEq(P2,P1)
l3coeff = get_TriEq(P0,P2)
xl = P0[0]
xr = P0[0]
dyl = P1[1]-P0[1]
dxl = P1[0]-P0[0]
dyr = P2[1]-P0[1]
dxr = P2[0]-P0[0]
px=[]
py=[]
px.append(P0[0])
py.append(P0[1])
miny=min(P0[1],P1[1],P2[1])
maxy=max(P0[1],P1[1],P2[1])
x=px[-1]
y=int(py[-1])
direc=1
if (dyl)<0: direc=-1
for i in range(int(maxy-miny)+2):
if (i<np.abs(dyl)+1) :
xl = int(np.floor((-l1coeff[1]*y-l1coeff[2])/l1coeff[0]))
else :
xl = int(np.floor((-l2coeff[1]*y-l2coeff[2])/l2coeff[0]))
xr = int(np.ceil((-l3coeff[1]*y-l3coeff[2])/l3coeff[0]))
y= int(P0[1]+i*direc)
for x in range(xl,xr+1):
if InsideCheck(x,y,l1coeff,l2coeff,l3coeff):
px.append(x)
py.append(y)
xl+=dxl/dyl
xr+=dxr/dyr
xl = int(np.floor(xl))
xr = int(np.ceil(xr))
plt.scatter(px,py)
plt.triplot([P0[0],P1[0],P2[0]],[P0[1],P1[1],P2[1]])
plt.show()









댓글
댓글 쓰기