[Introduction to Topology] 위상수학 Chapter1 집합 이론

 집합 이론

집합은 오래전부터 쓰던 수하적 표현 방법입니다. 이에 대부분의 수학적 표현을 집합을 통해서 합니다. 집합에 있어 중요한 것은 Notation과, 집합의 표현 방법들에 대하여 배우게 될 것입니다. 대표적으로 함수, 이미지, 관계에 대해 배울 것입니다.

    

간단한 예시를 보면 다음과 같은 포함 관계를 나타낼 수 있다. 

$$ (a,b)\subset [a,b] \subset \mathbb{R} $$

드모르간 법칙

$$C(A\cup B) = C(A) \cap C(B) $$

$$ C(A\cap B)=C(A)\cup C(B)$$

Indexed Family Set

Let $I$ 는 인덱스 집합이라고 하고, 각 $\alpha$가 I집합에 속한다. $\alpha\ \in I$. A가 S집합의 부분 집합이라하고, alpha의 인덱스를 가지고 있다면 다음과 같이 표현할 수 있다.

 $$A_\alpha \subset S$$ 

위의 표현은 alpha가 index 집합에 속해있으니, S 집합에서 s의 index family라 부른다. 집합적인 표현으로는 다음과 같이 나타낸다.

$$ \{A_\alpha \}_{ \alpha \in I }$$

$$\cup_{\alpha \in I} A_\alpha $$

교집합과, 합집합의 경우 Indexed Family 내에서도 동일하게 적용할 수 있다. 다만, 교집합의 경우 subset을 제외한 나머지 집합으로 여겨진다.

$$ \cup_{\alpha \in \{i,j\}}A_\alpha = A_i \cup A_j$$

$$ \cap_{\alpha \in \{i,j\}}A_\alpha = A_i \cap A_j$$

$$\cap_{\alpha \in \emptyset} A_{\alpha} = S$$

Products of SETS

집합에서의 Products 들은 Tuple 셋으로 나타난다. 이는 순서쌍인 형태인 (x,y)가 대표적이다.

$$A \times B , \text{ where } x \in A, y \in B$$

일반화 된 표현으로는 PI 오퍼레이터를 이용한다. 

$$(a_1,a_2,\cdots,a_n)$$

$$\text{where } a_1\in A_1, a_2\in A_2, \cdots a_n \in A_n $$

$$\Pi_{i=1}^n A_i , \text{ where }  A = A_1 \times A_2 \cdots \times A_n $$

Function, Graph and Image

함수와 그래프는 집합의 표현으로 나타낼 수 있다. 함수의 경우 A의 집합에서 B 집합으로 보낸다는 관점에서 Mapping 또는 transformation이라고도 한다. 여기서 A의 영역을 Domain, B의 영역을 Range라고 정의한다.

$$f: A \to B, x\in A, f(x) \in B $$

one to one (1:1) 매핑의 경우 injective 라고 한다. 이 경우 다음 과 같은 성질이 있다. 

$$f(a)=f(a'), a,a\in A, a=a'$$

$$f:A\to B, \text{if }B=f(A)$$

$$f:A\to B, b\in f(A), a \in A \to f(a)=b$$

그래프의 경우 한쌍의 형태로 나타난다. 예를 들어 직선의 경우 (1,1), (2,2), (3,3)과 같은 하나의 점좌표를 이은 형태이다. 즉, 그래프는 하나의 Tuple 형태로 나타난다는 것을 알 수 있다.

집합에서 함수 f에 대한 그래프 표기방법으로는 다음과 같이 나타낸다. 

$$ f: X\to Y $$

$$ \Gamma_f \subset X \times Y $$

이의 형태는 당연하게 (x,f(x)) 형태를 가지게 된다.

그래프의 경우 곡선의 형태로 나타난다. 반면, 이미지는 하나의 큰 집합 형태로 나타난다. 그래프의 경우 element들의 pair로 나타내었다면, 이미지는 집합 형태의 쌍으로 나타낸다.

$$\text{Let } f :A \to B $$ 

$$ X \subset A, f(X) \subset Y $$

여기서 그래프의 경우는 X에 포함된 x의 element로 나타낸다. 반면 이미지는 A의 부분집합의 모음집인 경우에 해당한다. (X,f(X)) : 이미지, (x,f(x)): 그래프

Relation

Relation 또한 순서쌍으로 나타난다.  A집합의 a 요소와 B집합의 b 요소에 대한 관계는 다음과 같이 표시하며, 대표적으로는 aRb 형태로 나타난다. 만약 크기 비교의 예시를 본다면 a<b가 될 수 있다. 이에 대한 관계 표시로는 (a,b)이다.

$$ A \times B $$

관계에는 4가지 특성을 분류할 수 있다.

• reflexive
• aRa is true, (ex. 1=1, |x-y| <1, |x-x|=0 <1, |y-y| =0 <1)

• symmetric
• 교환 법칙 aRb가 성립하면 bRa도 성립 (|x-y| = |y-x|)
• transitive
• 연쇄 법칙 (삼단 논법) aRb, bRc 이면 aRc가 만족
• $$ if \, a\to b \to c, then \, a \to c $$
• equivalence
• 위의 3가지 법칙이 적용되는 관계.
• $$\pi(a)로 표현 $$

Composition of function and diagrams

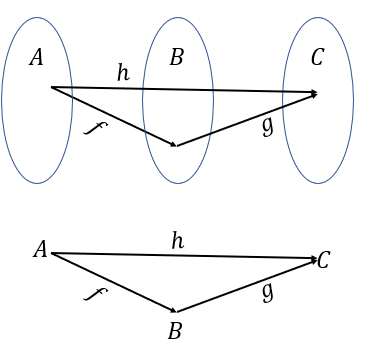
함수간의 관계는 Domain과 Range관계로 표시가 가능하다. 위의 그림은 간단하게 보이며, 이를 표현하는 방법도, 어렵지 않다. 이전에 함수의 관계로 본다면 h=fg와 같은 것을 알수 있다.

$$f:A\to B, g:B\to C, h: A \to C$$

이는 transitive 하는 특성이 있다. 대표적으로 합성함수가 이러한 형태 변환에 해당한다. 대표적으로는 치환하여 쉽게 푸는 형태이다.

$$h(x)=g(f(x))$$ 

당연하게 f(x)를 통해서 A에서 B를 보냈고, g(B)를 통해서 B에서 C를 보내는 과정은 A에서 C로보내는 과정인 h와 동일하다

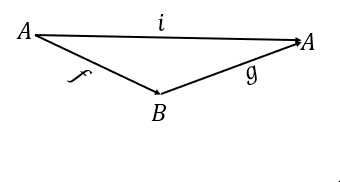
당연하게도 identity function이 존재하는데 이는 어떠한 집합에 대해서도 자기 자신으로 돌아오는 성질을 말한다. 대표적으로 +의 경우 0을 더하는 경우, 곱하기의 경우 1을 곱하는 경우로 생각해볼 수 있다. 

identity function은 역함수와 관련이 있다. 역함수는 어떠한 연산을 한 후 자기 자신을 나타내는 함수를 나타낸다. 여기서 g가 역함수에 해당한다. 대표적으로 다음과 같은 연산을 생각해 볼 수 있다.

$$ln(exp(x)=x$$

$$f(g(x))=x, \, f(x)=ax, \, g(x)=\frac{1}{a}$$